计算最小二乘回归:方程,例子,解释

能够做出结论关于数据的趋势是最重要的步骤之一,在商业和科学。的面包和黄油的市场分析师意识到特斯拉的股票炸弹Elon Musk每次出现在喜剧的播客,以及科学家计算需要多少火箭燃料驱动一辆车进入太空。
如何找到一个最小二乘回归
通常我们问的问题需要我们做出准确的预测之一因素影响一个结果。如果一个老师是问如何工作花时间写一篇文章影响论文的成绩,很容易看一个图的时间写论文和论文成绩说“嘿,花更多的时间在他们的论文的人得到更好的成绩。“什么是更加困难(和现实,很可能)眼睛是试着去做预测得到什么分数会有人在一篇基于他们花了多长时间。当然,还有其他因素在起作用就像特定类的学生有多好,但我们会忽视混淆现在这样的因素和工作通过一个简单的例子。
我们的老师已经知道有多少时间是花在一个积极的关系和年级作文一篇文章,但是我们需要一些数据正确地证明这一点。
最小二乘回归直线的例子
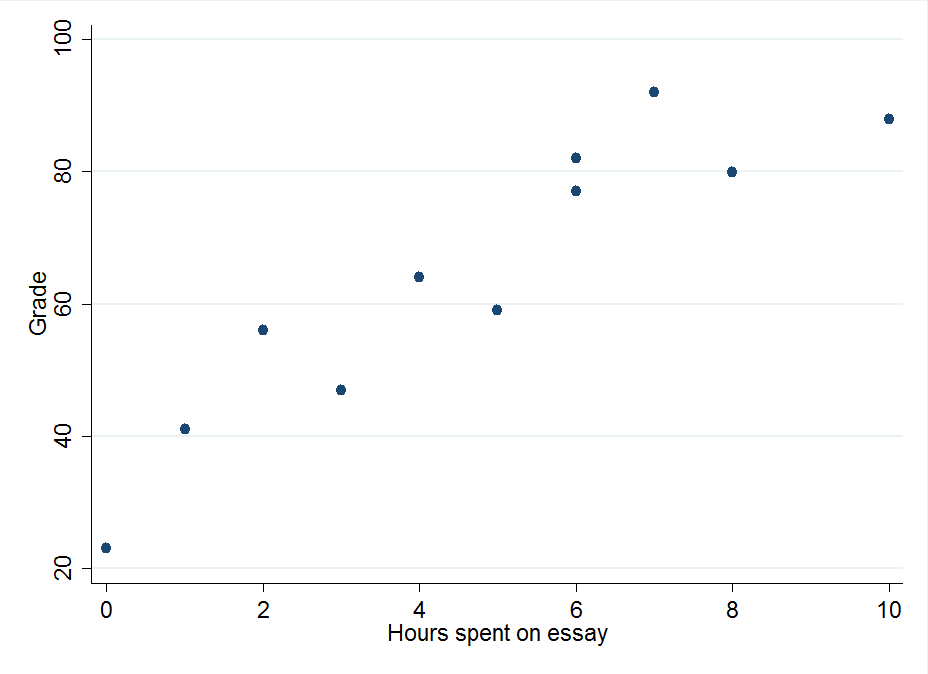

最小二乘回归方程

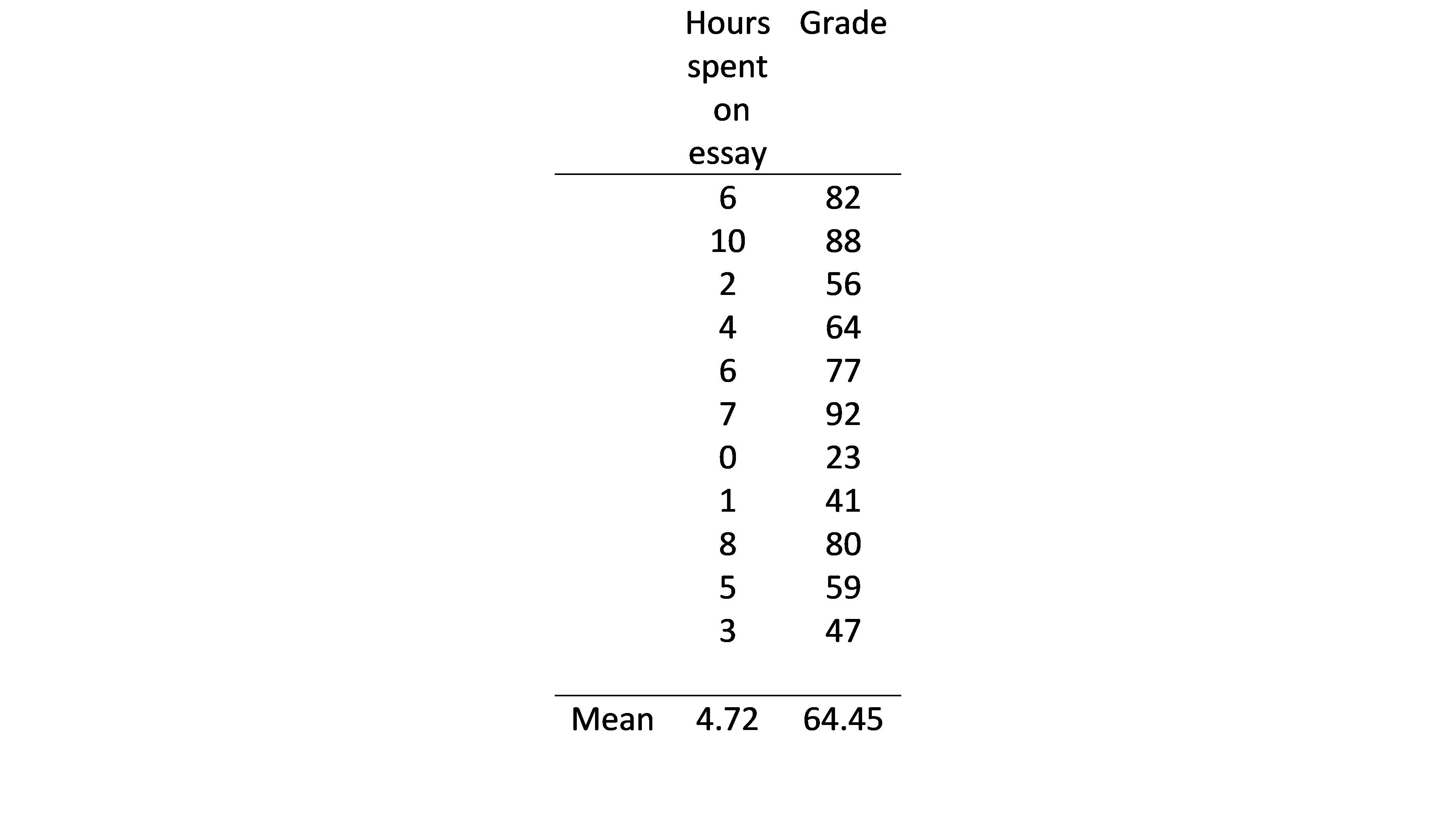
如何计算一个最小二乘回归行吗?
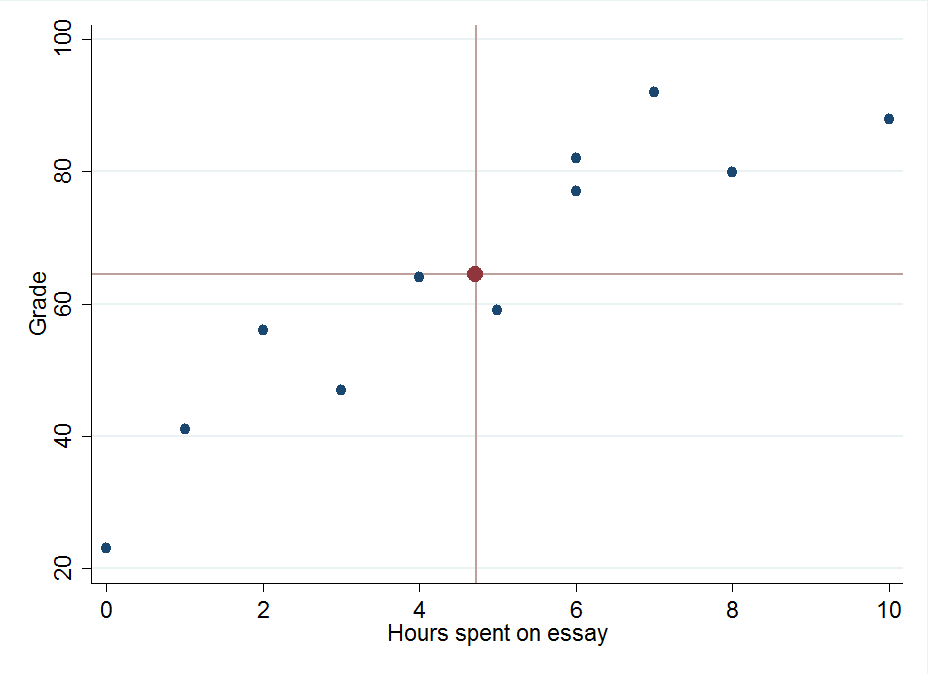
第二步是计算每个值和平均值的区别的依赖和独立变量。在这种情况下,这意味着我们从每个测试分数减去64.45和4.72从每个数据点的时间。此外,我们希望找到一起乘这两个不同的产品。

你应该注意一些分数低于平均得分,我们结束了负值。通过这些差异的棱角,我们最终得到一个标准化的测量的平均偏差不管值或多或少比的意思。
让我们提醒自己我们需要计算的方程b。
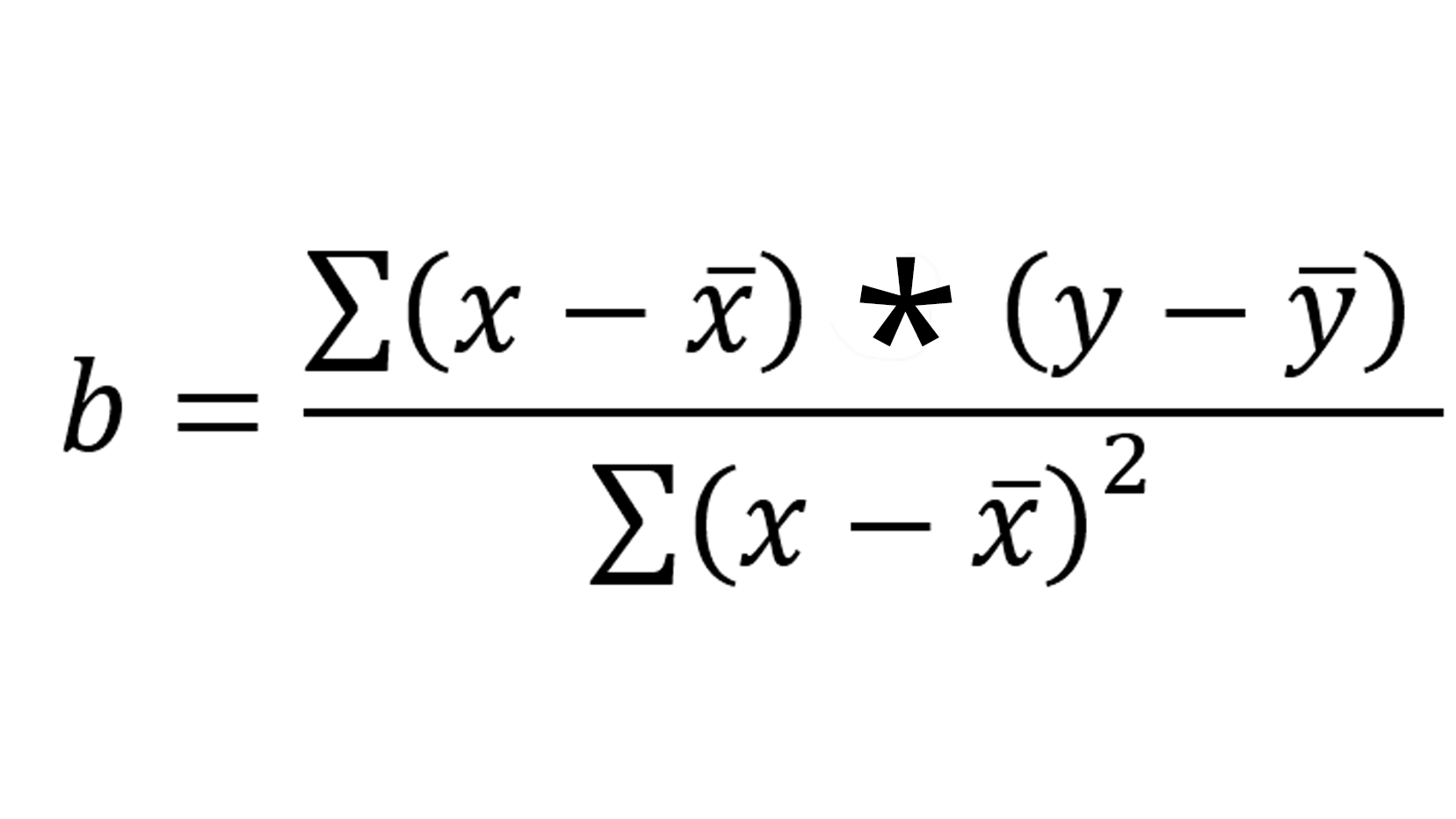
象征西格玛(∑)告诉我们我们一起需要添加所有相关的值。
如果我们做上面的表中,我们得到了以下结果:
∑(x̅) *(等号左边̅)= 611.36
和
∑(x̅) ^ 2 = 94.18
插在上面的信息从表到一个计算器允许我们计算b,这是一步两种开启我们的闪闪发光的新模型的预测能力:

最后一步是计算拦截,我们可以使用初始值的回归方程测试分数和时间设置为各自的含义,以及我们的新计算系数。
64.45 = 4.72 + 6.49 *
我们可以解决这个问题一个:
64.45 = 30.63 +
一个= 64.45 - 30.63
一个= 30.18
现在我们已经为我们的方程和所需的所有信息都是免费的值作为我们认为合适的位置。如果我们想知道预测年级花2.35小时的人的文章,我们需要做的就是在交换X。
y = 30.18 + 6.49 * X
y = 30.18 + (6.49 * 2.35)
y = 45.43
用手画一个最小二乘回归直线
如果我们想画一个最适合线,我们可以计算一系列的时间值的估计成绩,然后连接用一把尺子。正如我们前面所提到的,这条线应该交叉的文章所花费的时间和平均成绩。
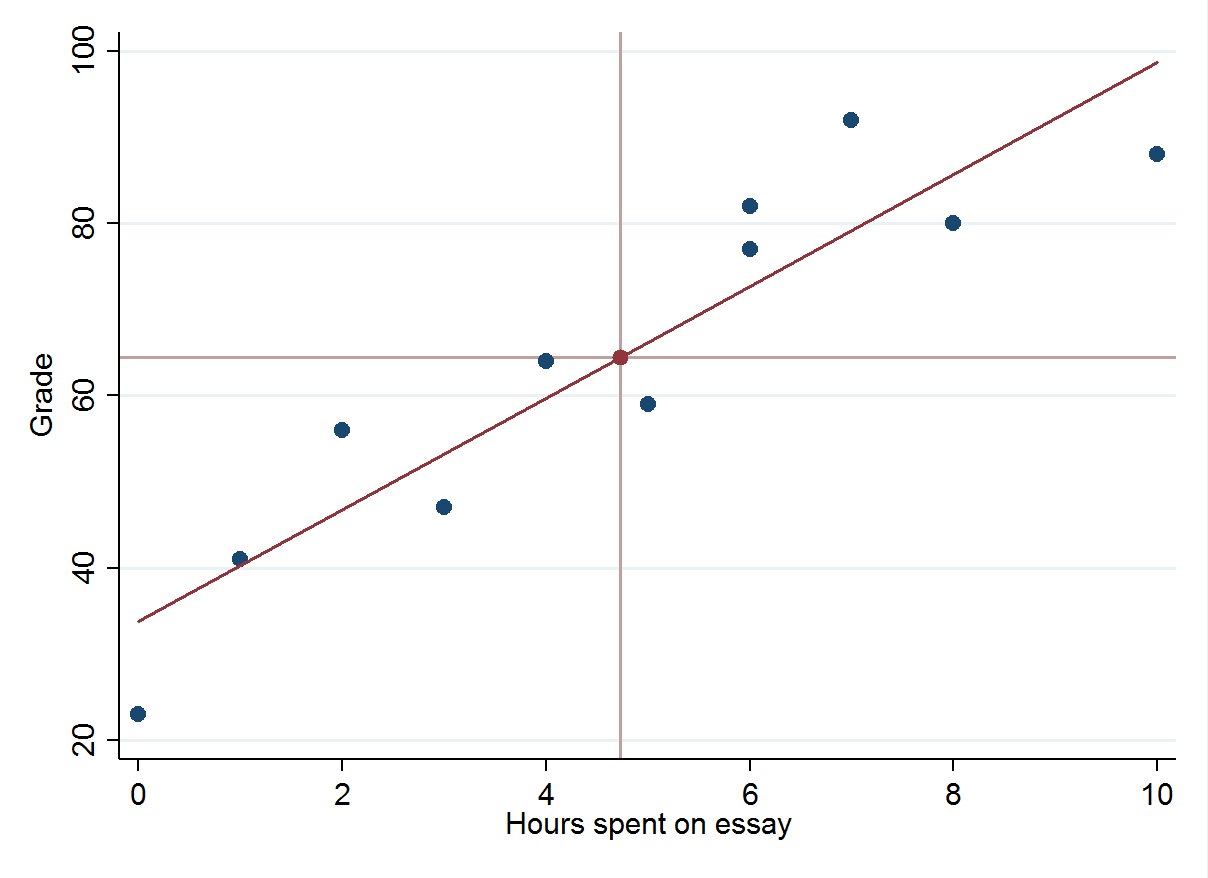
还有我们!完美的预测模型,将使我们的教师生活容易得多。
最小二乘回归的缺点是什么?
*大家可能已经注意到,这样一个模型有其局限性。例如,如果一个学生在一篇文章花了20个小时,他们的预测分数是160,并没有真正意义上一个典型的0 - 100的规模。它总是重要的了解现实的真实模型的局限性和确保它不被用来回答问题不适合。
这些异常值对我们的数据可以有一个不成比例的影响。在这种情况下,是很重要的组织你的数据并验证您的模型根据你的数据是什么样子,以确保它是正确的做法。
本文最初上传于10月2日,2020年8月21日,2018年,最后一次更新。



