二项检验

什么是二项式检验?

二项检验，有时也称为二项精确检验，是一种用于抽样统计的检验，用于评估二元变量的比例是否等于某些假设值。在本文中，我们将探讨该测试的关键特性，并介绍一个示例测试。

有时，您可能还希望测试总体比例的零假设是否大于特定的假设值(或小于)，而不是在任何方向上不同，在这种情况下，您将执行单侧显著性检验，但更常见的是使用双侧方法。

请注意，在二项式测试中没有生成测试统计量，而在其他统计测试(如曼-惠特尼U测试或者是非配对学生t检验，因为p值是直接计算的。

什么时候使用二项式检验

二项式检验用于调查感兴趣的二元变量(只能取两个可能值的变量，例如死亡率(死亡/活着))，并且你有一个假设或期望值来比较它。该测试只能在样本量相对于您试图进行推断的总体而言较小时使用。

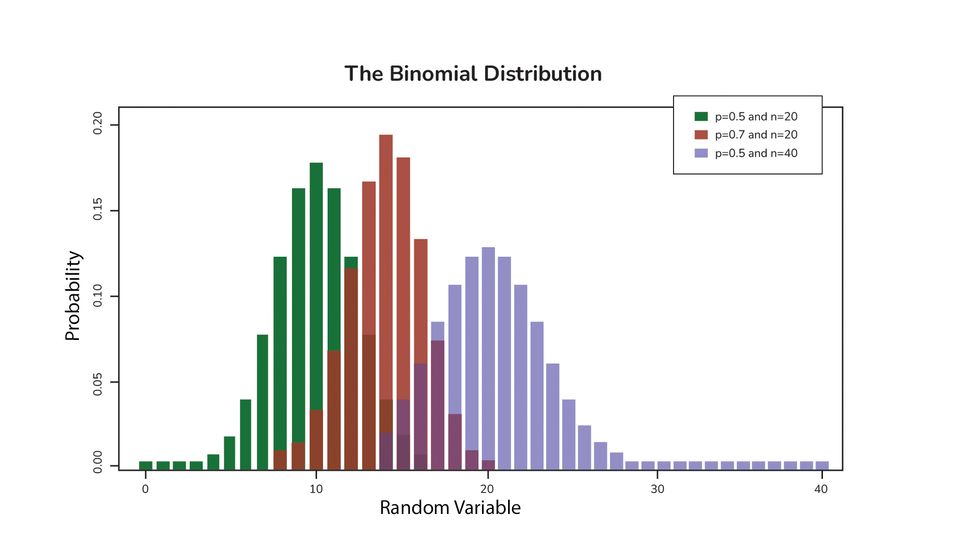
在成功比例p和试验次数n的不同值下，二项分布形状的变化。

二项检验来源于二项分布，二项分布可以被认为是“成功”或“失败”的数量达到一定数量后的分布，n重复的独立实验或“试验”。用更统计的语言来说，我们可以说分布依赖于的值n和p(任何试验成功的概率)这些是二项分布的参数。值得注意的是，作为样本大小(的值)n)增加，分布变得更加对称，并收敛为正态分布。

二项检验假设

二项检验的假设如下，可以很容易地使用“BINS”首字母缩写来记住:

• B -感兴趣的变量应该是a二进制结果意味着它只能采取两种值中的一种(例如，掷硬币(正面/反面)，是否存在疾病(是/否)，道德(死/活))。这有时也被称为二分类变量。
• 我的观察应该是独立的这意味着一个观测值不应该对另一个观测值的概率有任何影响。
• N -实验应该有一个固定的样本量表示n．
• 所有独立的观测都应该有相同概率有了结果。这与独立性假设类似，可以通过随机抽样来实现。

二项测试示例

假设一名人口健康研究人员进行了一项小型随机抽样调查，以估计单纯疱疹病毒(HSV)的患病率(受影响人口的比例)，这是一种引起生殖器和口腔疱疹的常见病毒感染。样本的成员是随机抽取的，总共有20人(n=20)，彼此独立且具有相同结果的概率，并且具有感兴趣的二元结果(存在HSV;是的/不)。

因此，我们可以将其概念化为一系列20个独立试验，其中感染人数的比例p，遵循二项分布。假设在调查中发现20名参与者中有6人(30%)患有HSV。因此，一个给定的调查参与者患这种疾病的概率是p=0.3。假设之前的一项调查发现HSV的患病率为20%(这可能来自相同的人群或类似的人群)——研究人员将其作为假设值，在此基础上对当前的调查比例进行二项式检验。

下一步是运行二项检验并生成p值，它表示HSV患者比例达到极端或比观察到的情况更极端的概率p等于假设值。可以依靠统计软件包(如Stata、SPSS或R Studio)来生成Binomial检验p值，但为了说明目的，公式详细如下。如果我们有n有HSV可能性的独立试验p我们可以计算该值为假设的HSV病例数的概率，r(在这种情况下)r=4, 20的20% =4)，使用下式:

通过将这些值代入二项式公式，我们得到0.196，即20例中有6例或更少HSV病例的概率(单尾检验)。因为我们感兴趣的假设是观察值和假设值是否在任何方向上不同，所以我们想要生成双尾检验，所以我们乘以2得到最终的p值0.392。

使用显著性水平α=0.05我们不能拒绝原假设，因为p > 0.05，并得出结论，在给定样本量的情况下，没有证据表明本次调查中HSV的患病率与上次调查相比有统计学上的显著差异。

Elliot McClenaghan是伦敦卫生与热带医学学院流行病学和医学统计研究员